Area of a Triangle

An earlier section, Area Formulas: Triangle, Parallelogram, Trapezoid , showed how to find the area of a triangle with a base/height pair. The key results are summarized here for convenience.

With trigonometry now in hand, another useful formula for the area of a triangle is given.

Area of a Triangle using a Base/Height Pair
Area of a Triangle using Two Sides and an Included Angle

AREA OF A TRIANGLE USING A BASE/HEIGHT PAIR

Take a vertex of a triangle.
Drop a perpendicular to the opposite side or (if needed) to an extension of the opposite side.
The segment just created is called a height or altitude of the triangle. The side opposite the vertex is called the corresponding base.
Since every triangle has three vertices, every triangle has three base/height pairs .
Area is half base times height: $$ \begin{gather} \cssId{s14}{\text{area of triangle}}\cr \cssId{s15}{\text{with base $\,b\,$ and height $\,h\,$}}\cr \cssId{s16}{= \frac 12 bh} \end{gather} $$

Drop a perpendicular to the opposite side ...

... or, to an extension of the opposite side.

A derivation of the triangle area formula ($\,bh/2\,$) was given in
Area Formulas: Triangle, Parallelogram, Trapezoid for the situation
where the altitude ‘hits’ the base (left-most picture above).

The formula also works when the altitude doesn't ‘hit’ the base,
but instead hits an extension of the base, as shown at right.
Here's how:

Suppose you want the area of the blue triangle at right ($\,\triangle ABC\,$).
This triangle has base $\,b\,$ and height $\,h\,.$
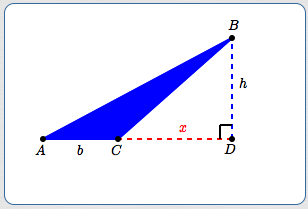
Let $\,x\,$ denote the length of the red-dashed segment.

Then: $$ \begin{align} &\cssId{s26}{\text{area of blue triangle}}\cr\cr &\qquad \cssId{s27}{= \quad \text{area of big right triangle } (\triangle ABD) - \text{area of small right triangle } (\triangle CBD)}\cr\cr &\qquad \cssId{s28}{= \quad \frac 12(b+x)h - \frac 12 xh}\cr\cr &\qquad \cssId{s29}{= \quad \frac 12bh + \frac 12xh - \frac 12xh}\cr\cr &\qquad \cssId{s30}{= \quad \frac 12bh} \end{align} $$

area of blue triangle is $\,\frac 12 bh\,$

Note that there are infinitely many triangles with a given base/height pair.
For example, all the triangles below have the same base/height pair.
Same base/height pair—same area!
A base/height pair uniquely determines the area of a triangle, but not the shape of the triangle.


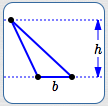
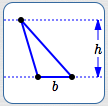
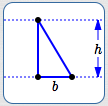
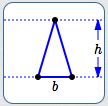
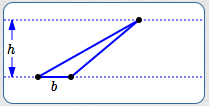
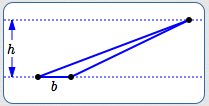
All these triangles have the same base/height pair, hence the same area.

AREA OF A TRIANGLE USING TWO SIDES AND AN INCLUDED ANGLE

By the SAS (side-angle-side) triangle congruence theorem,
two sides and an included angle uniquely defines a triangle.

Let $\,a\,$ and $\,b\,$ denote two sides of a triangle,
with included angle $\,\theta\,.$

The sketches at right and below show the two situations that can occur when finding the altitude that has corresponding base $\,b\,.$ In both cases, the altitude length is found using the yellow triangle (which is a right triangle with hypotenuse $\,a\,$).

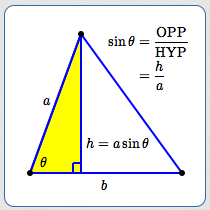
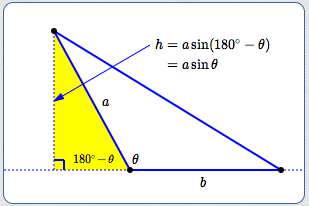
In both cases, the altitude length is $\,h = a\sin\theta\,.$

Thus: $$ \begin{align} &\cssId{s45}{\text{area of triangle with sides $a$ and $b$ and included angle $\theta$}}\cr\cr &\qquad \cssId{s46}{= \frac 12(\text{base})(\text{height})}\cr\cr &\qquad \cssId{s47}{= \frac 12 b(a\sin\theta)}\cr\cr &\qquad \cssId{s48}{= \frac 12 ab\sin\theta} \end{align} $$ In words, the area is:

half the product of the two sides,
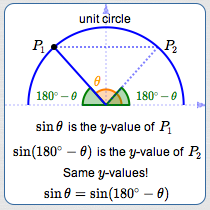
times the sine of the included angle

(When we write $\,180^\circ - \theta\,,$ it is assumed that $\,\theta\,$ is measured in degrees.)

Master the ideas from this section
by practicing the exercise at the bottom of this page.

When you're done practicing, move on to:
Law of Sines