 Area of a Circular Sector
Area of a Circular Sector
If you studied the earlier section, Length of a Circular Arc, then this section will seem familiar and comfortable.
The same techniques used to find arc length are now used to find the area of a sector of a circle.
As shown below, a central angle determines a ‘piece’ of a circle—which looks like a piece of pie, if the angle isn't too big. These pieces are referred to as sectors of the circle.
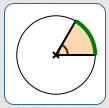
Computing the area of a sector is simple: find the desired fraction ($\frac{\text{part}}{\text{whole}}$) of the total area! Central angles are used to determine the desired fraction.
Be sure to use the same angle units for the ‘part’ and the ‘whole’, so that units cancel (as needed).
Here are examples. Let $\,A\,$ denote the total area of a circle.
$$ \begin{align} &\cssId{s11}{\text{Sector area with central angle $\,180^\circ\,$}}\cr\cr &\qquad\cssId{s12}{= \frac{180^\circ}{360^\circ}\cdot A}\cr\cr &\qquad\cssId{s13}{= \frac{180}{360}\cdot A \qquad \text{(units cancel)}}\cr\cr &\qquad\cssId{s14}{= \frac{1}{2}A} \end{align} $$$$ \begin{align} &\cssId{s15}{\text{Sector area with central angle $\,90^\circ\,$}}\cr\cr &\qquad\cssId{s16}{= \frac{90^\circ}{360^\circ}\cdot A}\cr\cr &\qquad\cssId{s17}{= \frac{1}{4}A} \end{align} $$
$$ \begin{align} &\cssId{s18}{\text{Sector area with central angle $\,60^\circ\,$}}\cr\cr &\qquad\cssId{s19}{= \frac{60^\circ}{360^\circ}\cdot A}\cr\cr &\qquad\cssId{s20}{= \frac{1}{6}A} \end{align} $$
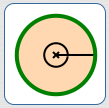
$$\text{Total area of circle} = A$$
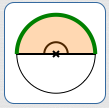
$$ \begin{align} &\text{Sector area}\cr &\quad = \frac{180^\circ}{360^\circ}\cdot A\cr &\quad = \frac{1}{2}A \end{align} $$
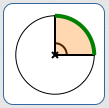

The Sector Area is a Desired Fraction of the Total Area
$$ \begin{align} &\cssId{s26}{\text{Sector Area}}\cr\cr &\qquad \cssId{s27}{= (\text{Desired Fraction})(\text{Total Area of Circle})}\cr\cr &\qquad \cssId{s28}{= \left( \frac{ \substack{ \text{Central Angle} \\ \ \ \text{Corresponding to}\ \ \\ \text{Desired Sector} \\ \vphantom{y} }} { \substack{ \vphantom{C}\\ \text{Central Angle}\strut \\ \text{Corresponding to} \\ \text{Total Area} }} \right) \cdot (\text{Total Area of Circle})} \end{align} $$Area of a Circular Sector: Using Degree Measure for Central Angle
In degree measure, one complete revolution is $\,360^\circ\,.$
The area of a circle with radius $\,r\,$ is $\,\pi r^2\,.$ The number $\,\pi\,$ has no units. Therefore, the unit for area is the unit of $\,r\,,$ squared.
For example, if $\,r\,$ is measured in feet, then area has units of square feet:
$$ \cssId{s35}{(\text{feet})^2 = \text{ft}^2} $$Don't ever lose sight of just how much area one square foot represents! It is a square, where each side has length $\,1\,$ foot.
Let $\,\theta\,$ be a real number, without units, that represents the degree measure of a central angle. For example, if $\,\theta = 60\,,$ then $\,\theta^{\,\circ} = 60^\circ\,.$
The area of the sector corresponding to $\,\theta\,$ is computed as follows:
$$ \begin{align} &\cssId{s41}{\text{Sector Area}}\cr\cr &\qquad \cssId{s42}{= \left( \frac{ \substack{ \text{Central Angle} \\ \ \ \text{Corresponding to}\ \ \\ \text{Desired Sector} \\ \vphantom{y} }} { \substack{ \vphantom{C}\\ \text{Central Angle}\strut \\ \text{Corresponding to} \\ \text{Total Area} }} \right) \cdot (\text{Total Area})}\cr\cr &\qquad \cssId{s43}{= \frac{\theta^{\,\circ}}{360^\circ}(\pi r^2)}\cr\cr &\qquad \cssId{s44}{= \frac{\theta}{360}(\pi r^2)}\cr\cr \end{align} $$Equivalently, we can use a proportion. Think of the whole circle as the sector corresponding to $\,360^\circ\,$:
$$ \begin{gather} \cssId{s47}{\frac{\text{Part Angle}}{\text{Whole Angle}} = \frac{\text{Part Area}}{\text{Whole Area}}}\cr\cr \cssId{s48}{\frac{\theta^{\,\circ}}{360^\circ} = \frac{\text{Sector Area}}{\pi r^2}} \end{gather} $$Cancel the degree units on the left, cross-multiply, and solve for the desired area:
$$ \begin{gather} \cssId{s50}{\pi r^2\theta = 360(\text{Sector Area})}\cr\cr \cssId{s51}{\text{Sector Area} = \frac{\pi r^2\theta}{360}}\cr\cr \end{gather} $$Summary: Area of a Circular Sector when Central Angle is Measured in Degrees
There is a subtle but annoying issue that arises in the formula using degree measure, as follows.
Say you want the sector area corresponding to a central angle of $\,60^\circ\,.$ You want to use the variable $\,\theta\,$ to ‘hold’ this central angle information.
You have two choices:
- Let $\,\theta\,$ hold both the size and the unit: i.e., let $\,\theta = 60^\circ\,.$
- Let $\,\theta\,$ hold only the (real number) size: i.e., let $\,\theta = 60\,,$ in which case $\,\theta^{\,\circ} = 60^\circ\,.$
Both ways will work, but they give rise to slightly-different-looking formulas.
Above, choice (2) was used, yielding the formula:
$$ \cssId{s63}{\text{Sector Area} = \frac{\pi r^2\theta}{360}} $$For choice (1), the degree units can't be cancelled, since the unit is ‘trapped’ inside the variable $\,\theta\,.$ In this case, the formula becomes:
$$ \cssId{s66}{\text{Sector Area} = \frac{\pi r^2\theta}{360^\circ}} $$Of course, when you put
- $\,\theta = 60\,$ into the formula $\displaystyle \frac{\pi r^2\theta}{360}$
- $\,\theta = 60^\circ\,$ into the formula $\displaystyle \frac{\pi r^2\theta}{360^\circ}$
you get precisely the same result! Make your choice, and use the appropriate formula!
Area of a Circular Sector: Using Radian Measure for Central Angle
In radian measure, one complete revolution is $\,2\pi\,.$
Recall that the radian measure of an angle is a real number. Radian measure has no units. Consequently, there are no annoying issues in the formula for sector area when the central angle is measured in radians. Hooray!
Let $\,\theta\,$ be the radian measure of a central angle. The sector area corresponding to $\,\theta\,$ is computed as follows:
$$ \begin{align} &\cssId{s80}{\text{Sector Area}}\cr\cr &\qquad \cssId{s81}{= \left( \frac{ \substack{ \text{Central Angle} \\ \ \ \text{Corresponding to}\ \ \\ \text{Desired Sector} \\ \vphantom{y} }} { \substack{ \vphantom{C}\\ \text{Central Angle}\strut \\ \text{Corresponding to} \\ \text{Total Area} }} \right) \cdot (\text{Total Area})}\cr\cr &\qquad \cssId{s82}{= \frac{\theta}{2\pi}(\pi r^2)}\cr\cr &\qquad \cssId{s83}{= \frac 12 r^2\theta} \end{align} $$Equivalently, we can use a proportion:
$$ \begin{gather} \cssId{s85}{\frac{\text{Part Angle}}{\text{Whole Angle}} = \frac{\text{Part Area}}{\text{Whole Area}}}\cr\cr \cssId{s86}{\frac{\theta}{2\pi} = \frac{\text{Sector Area}}{\pi r^2}}\cr\cr \end{gather} $$Cross-multiply and solve for the desired area:
$$ \begin{gather} \cssId{s88}{\pi r^2\theta = 2\pi (\text{Sector Area})}\cr\cr \cssId{s89}{\text{Sector Area} = \frac 12 r^2\theta} \end{gather} $$Summary: Area of a Circular Sector when Central Angle is Measured in Radians
$$ \cssId{s91}{\text{Sector Area} = \frac 12 r^2\theta} $$As an alternative to the degree-measure derivation given above, we can ‘convert’ the formula to one that works for central angles measured in degrees, as follows.
First, convert $\,\theta^{\,\circ}\,$ to radian measure. Since $\pi\,$ radians equals $\,180^\circ\,,$ we have:
$$\cssId{s95}{1 = \frac{\pi}{180^\circ}}$$Therefore:
Thus, $\,\displaystyle\frac{\pi\theta}{180}\,$ is the radian measure of $\,\theta^{\,\circ}\,.$
Substitute this radian measure into the sector area formula:
$$ \begin{align} &\cssId{s100}{\text{Sector Area}}\cr\cr &\qquad \cssId{s101}{= \frac 12 r^2(\text{radian measure of $\theta$})}\cr\cr &\qquad \cssId{s102}{= \frac 12 r^2 \left(\frac{\pi\theta}{180}\right)}\cr\cr &\qquad \cssId{s103}{= \frac{\pi r^2\theta}{360}} \end{align} $$which, of course, is the same formula derived above.