Introduction to Polynomials
Introduction to Polynomials
Before doing this exercise, you may want to review the definitions of sums and terms.
There is an extremely important family of functions in mathematics, called polynomials.
Polynomials are easy to work with mathematically, because they are made up of very simple ‘pieces’, as discussed below.
Here's one reason that polynomials are so important:
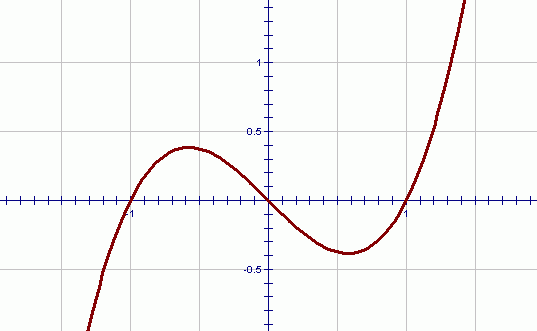
There is a famous theorem that says that any function on an interval $\,[a,b]\,$ with no breaks in its graph can be approximated as closely as desired by a polynomial.
That is, suppose you can trace the graph of a function from $\,x=a\,$ to $\,x=b\,$ without ever lifting up your pencil. Then, you can take the graph (no matter how ugly it is; no matter how complicated the formula that may describe it) and draw an ‘envelope’ around it—an envelope that is as ‘tight’ as we want—and get a polynomial that will live entirely inside this envelope.
(The polynomial that we get, however, may be very curvy and have many terms!)
An ‘envelope’ around a function;
we can get a polynomial inside!
A polynomial is a finite sum of terms, each of the form $\,ax^k\,,$ where $\,a\,$ is a real number, and $\,k\,$ is a nonnegative integer. That is, $\,k\in \{0,1,2,3,\ldots\}\,.$
The standard form of a polynomial is:
$$ \cssId{s24}{a_nx^n + a_{n-1}x^{n-1} + \cdots + a_1 + a_0} $$Here, $\,n\,$ denotes the highest power to which $\,x\,$ is raised; this highest power is called the degree of the polynomial. Thus, in standard form, the highest power term is listed first, and subsequent powers are listed in decreasing order.
Notice that in the notation $\,a_ix^i\,$ (read as ‘$\,a\,$ sub $\,i\,$ times $\,x\,$ to the $\,i\,$’), the number $\,a_i\,$ denotes the coefficient of the $\,x^i\,$ term.
The number $\,a_n\,,$ which is the coefficient of the highest power term, is called the leading coefficient of the polynomial.
Note that a constant (like $\,5\,$) can be written as $\,5x^0\,.$ This is why the power is allowed to equal zero in the definition of polynomial—to allow for constant terms.
Example: A Polynomial
The expression $\,\displaystyle 3-x^2 + \frac{2x^4}{9} + \sqrt{7}\,x\,$ is a polynomial.
The terms are: $\,3\,,$ $\,-x^2\,,$ $\,\displaystyle\frac{2x^4}{9}\,,$ and $\,\sqrt{7}\,x\,.$
Comparing each term with the required form $\,ax^k\,,$ we have:
| term | writing in the form $\,ax^k\,$ | $a$ | $k$ |
| $3$ | $\,3=3x^0$ | $a=3$ | $k=0$ |
| $-x^2$ | $-x^2 = (-1)x^2$ | $a=-1$ | $k=2$ |
| $\displaystyle\frac{2x^4}{9}$ | $\displaystyle\frac{2}{9}x^4$ | $\displaystyle a=\frac{2}{9}$ | $k=4$ |
| $\sqrt{7}\,x$ | $(\sqrt{7})\,x^1$ | $a=\sqrt{7}$ | $k=1$ |
Notice that every value of $\,a\,$ is a real number, and every value of $\,k\,$ is a nonnegative integer.
The standard form of this polynomial is: $$\cssId{s66}{\frac{2}{9}x^4 - x^2 + \sqrt{7}\,x +3}$$
Here, the highest power term is written first, and subsequent terms decrease in power. The degree is $\,4\,,$ since this is the highest power. The leading coefficient is $\,\frac{2}{9}\,,$ since this is the coefficient of the highest power term.
Notice that the leading coefficient actually leads (comes at the beginning of) the polynomial, only when the polynomial is written in standard form.
Example: Non-Polynomials
The following expressions are not polynomials:
- $\displaystyle\frac{1}{x}=x^{-1}\,$ is not a polynomial; no negative powers are allowed
- $\sqrt{x} = x^{1/2}\,$ is not a polynomial; the number $\,\frac{1}{2}\,$ is not an allowable power
-
$\cssId{s79}{\sqrt{7x}} \cssId{s80}{= \sqrt{7}\cdot\sqrt{x}} \cssId{s81}{= \sqrt{7}x^{1/2}}\,$ is not a polynomial; the number $\,\frac{1}{2}\,$ is not an allowable power
Make sure you see the difference between $\,\sqrt{7}\,x\,$ (a polynomial) and $\,\sqrt{7x}\,$ (not a polynomial).
A polynomial with exactly one term is called a monomial.
A polynomial with exactly two terms is called a binomial.
A polynomial with exactly three terms is called a trinomial.
A polynomial of degree $\,2\,$ is called a quadratic function.
A polynomial of degree $\,3\,$ is called a cubic function.
A polynomial of degree $\,4\,$ is called a quartic function.
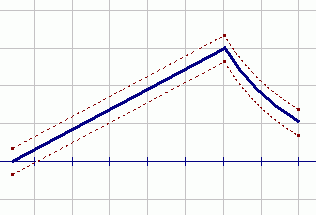
Polynomials have beautiful smooth graphs—no breaks and no kinks. The higher the degree of a polynomial, the more it is allowed to ‘turn’ (change direction). Indeed, it can be shown easily (using calculus) that a polynomial of degree $\,n\,$ can have at most $\,n-1\,$ turning points.
The graph below is the polynomial $\,P(x)=x^3 - x\,.$ Notice that this polynomial has degree $\,3\,$ and has $\,2\,$ turning points.